Wybór solveru CalculiXa do rozwiązywania układów równań równowagi i jego optymalizacja
1
Wprowadzenie
Najwięcej czasu przy analizie MES zajmuje rozwiązywanie układu równań równowagi. CalculiX ChunchiX może być używany z kilku solverami tego typu. Niżej najpierw będzie podana zostanie charakterystyka każdego z nich. Dalej solvery te zostana porównane na przykładzie prostego zagadnienia liniowego 3D.
2
Opis solverów do rozwiązywania układu równań liniowych
2.1
Interative Cholesky
| Typ |
Iteracyjny |
| Licencja |
GPL |
| Opis |
Jako solver iteracyjny wymaga relatywnie mało pamięci RAM. Dla pewnej wąskiej klasy zagadnień (przykład będzie niżej) może być najszybszym, ale to zdarza się niezwykle rzadko. Nie jest w stanie użyć więcej niż jednego rdzenia procesora, z tego powodu jest dość przestarzały. |
| Zalecenie |
Używaj tylko do bardzo dużych zagadnień, w których w przypadku innych solverów macierz sztywności nie zmieściła się do pamięci RAM. |
2.2
Interative Scaling
| Typ |
Iteracyjny |
| Licencja |
GPL |
| Opis |
W porównaniu do Interative Cholesky jest zauważalnie wolniejszy, ale wymaga jeszcze mniej pamięci RAM. Nie jest w stanie użyć więcej niż jednego rdzenia procesora, z tego powodu jest dość przestarzały. |
| Zalecenie |
Ciężko wyobrazić sobie sytuację kiedy ten solver jest przydatny. |
2.3
Intel® Pardiso
| Typ |
Bezpośredni (direct) albo dokładny |
| Licencja |
Intel® Simplified Software Licence |
| Opis |
Prawdopodobnie najszybszy na świecie solver komercyjny  . Licencja na niego została wykupiona przez Intel od pierwotnego producenta i zoptymalizowana pod procesory tejże firmy. Jest obecnie częścią darmowej biblioteki Intel openAPI MKL. To jest ten sam solver, który w SOLIDWORKS Simulation nazywa się Intel Direct Sparse. "Wyciska" maksimum z procesorów Intela, niestety ma niższą wydajność w przypadku procesorów AMD. . Licencja na niego została wykupiona przez Intel od pierwotnego producenta i zoptymalizowana pod procesory tejże firmy. Jest obecnie częścią darmowej biblioteki Intel openAPI MKL. To jest ten sam solver, który w SOLIDWORKS Simulation nazywa się Intel Direct Sparse. "Wyciska" maksimum z procesorów Intela, niestety ma niższą wydajność w przypadku procesorów AMD. |
| Zalecenie |
Łączy w sobie szybkość i niezawodność dla wszystkich typów zagadnień, do których nadaje się CCX. Jeżeli zagadnienie nie udało się rozwiązać za pomocą szybszego solvera PasTiX, to następnym wyborem ma być Pardiso. W wersji OOC (out-of-core) jest jedynym ze wszystkich solverów, który pozwala rozwiązać zagadnienia tak duże, ze nie mieszczą się one do pamięci RAM. |
2.4
PasTiX
| Typ |
Mieszany: dokładny + iteracyjny |
| Licencja |
GPL |
| Opis |
Obecnie jest to najnowszy, najszybszy a jednocześnie kompletnie darmowy solver, dostępny w źródłach (open source). Zwykle jest szybszy od Pardiso tym więcej im większy jest układ równań. Dodatkowo potrafi używać procesor karty graficznej, ale tylko dla bardzo zaawansowanych kart Nvidia z przynajmniej 32GB wbudowanej pamięci. W takim przypadku daje dodatkowe przyspieszenie szybkości obliczeń od 4 do 8 razy. |
| Zalecenie |
Najlepiej ustawić go solverem domyślnym w PrePoMax. Niestety wymaga żeby układ równań mieścił się do pamięci RAM. W przypadku niepowodzenia używamy wolniejszego, ale niezawodnego Pardiso. |
2.5
SPOOLES
| Typ |
Bezpośredni (direct) albo dokładny |
| Licencja |
GPL |
| Opis |
Wolny i nie rozwijany od 1999 roku solver. Tradycyjnie był domyślnym w CCX do pojawienia się PasTiX. |
| Zalecenie |
Można go używać tylko dla najprostszych modeli z małą liczbą węzłów, kiedy czas obliczeń nie jest istotny. Realnie PasTiX i Pardiso są nieporównywalnie szybsze. |
2.6
Podsumowanie
Staraj się zawsze używać PasTiX, w przypadku problemów – Pardiso.
3
Jakie solvery i inne dodatki zawiera każdy z plików CCX
Na stronie nadrzędnej  są dwie wersję programu CalculiX CrunchiX:
są dwie wersję programu CalculiX CrunchiX:
- ccx_pastix_exodus.exe — podstawowa wersja programu z następującymi solverami: PasTiX (domyślny), SPOOLES, Iterative Choleski i Iterative Scaling. Dodatkowo ten plik zawiera:
- Interfejs do programu MFront
 , który pozwala definiować bardziej skomplikowane modele materiału, niż te, co dostępne w CCX
, który pozwala definiować bardziej skomplikowane modele materiału, niż te, co dostępne w CCX
- Możliwość zapisu wyników nie w domyślnym formacie CalculiXa FRD, lecz w bardziej uniwersalnym formacie Exodus II. Pozwala to np. wyświetlać i analizować wyniki uzyskane za pomocą CCX w bardziej zaawansowanych niż PrePoMax postprocesorach, np. takich jak darmowy Paraview
 . PrePoMax używa te same biblioteki graficzne co Paraview i może być uważany jego bardzo okrojoną wersją.
. PrePoMax używa te same biblioteki graficzne co Paraview i może być uważany jego bardzo okrojoną wersją.
Uruchamiamy program z zapisem wyników w formacie Exodus II za pomocą pliku wsadowego ccx_win*_exodus.cmd .
- ccx_MKL.exe — dodatkowa wersja programu zawierająca solver Intel® Pardiso i pozwalająca na rozwiązywanie szczególnie dużych układów równań.
4
Porównanie różnych solverów na przykładzie prostego statycznego zagadnienia 3D
4.1
Zadanie testowe
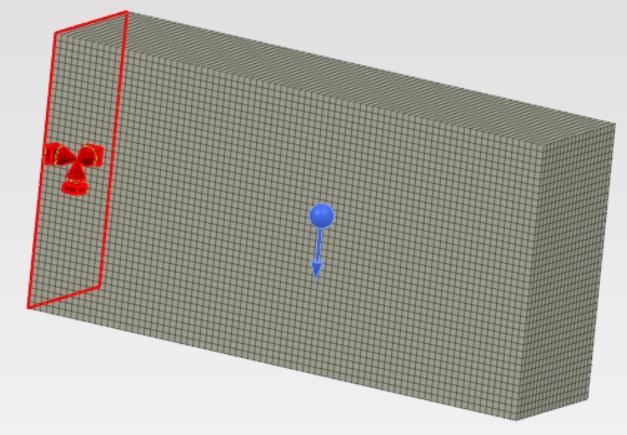 |
| Rys. 1. Schemat zagadnienia testowego. |
Zadanie testowe (Rys. 1) pochodzi z bardzo dobrego zestawu przykładów  wykorzystania CCX opracowanego przez prof. M.Kraskę z Brandenburg University of Applied Sciences. Jest to krótka belka wspornikowa poddana obciążeniu grawitacyjnemu.
wykorzystania CCX opracowanego przez prof. M.Kraskę z Brandenburg University of Applied Sciences. Jest to krótka belka wspornikowa poddana obciążeniu grawitacyjnemu.
 |
| Rys. 2. Minimalna gęstość siatki (27 950 stopni swobody). |
 |
| Rys. 3. Maksymalna gęstość siatki (414 470 stopni swobody). |
Zagadnienie to było rozwiązywane na 4 różnych siatkach składających się z elementów sześciennych 20-węzłowych z liczbą stopni swobody (równań równowagi) od 27 950 do 414 470 (Rys. 3)).
4.2
Wpływ liczby wątków procesora na czas rozwiązywania zagadnienia
Nowoczesne procesory składają się z więcej niż jednego rdzenia, a w każdym rdzeniu można uruchomić więcej niż jeden (zwykle 2) proces obliczeniowy (wątek). CalculiX jest w stanie wykorzystywać wielowątkowe procesory i prowadzić równoległe obliczenia na trzech następujących etapach rozwiązywania zagadnienia MES:
- Obliczenia macierzy sztywności pojedynczych elementów
- Rozwiązywania układu równań równowagi
- Obliczenia odkształceń i naprężeń w poszczególnych elementach
Użytkownik może ustalić ogólną liczbę wykorzystywanych wątków na każdym z tych etapów za pomocą zmiennych środowiskowych CCX_NPROC_STIFFNESS, OMP_NUM_THREADS i CCX_NPROC_RESULTS odpowiednio. Każda z tych zmiennych może przyjmować wartości od 1 do maksymalnie możliwiej dla danego procesora liczby wątków, którą zwykle określa zmienna środowiskowa NUMBER_OF_PROCESSORS. Zwykle jest to liczba rdzeni procesora razy 2.
Jaka jest optymalna liczbą wątków obliczeniowych dla CCX? Odpowiedź na to pytanie w przypadku systemu operacyjnego Windows nie jest prosta. System ten w moment startu uruchamia dziesiątki programów dodatkowych typu sterowników urządzeń zewnętrznych, programów do połączenia z siecią itp. Wszystkie one obciążają procesor i mają wyższy priorytet niż programy uruchomiane przez użytkownika. Więc sytuacja, w której cała moc procesora jest ciągle wykorzystywana przez program MES jest praktycznie niemożliwa.
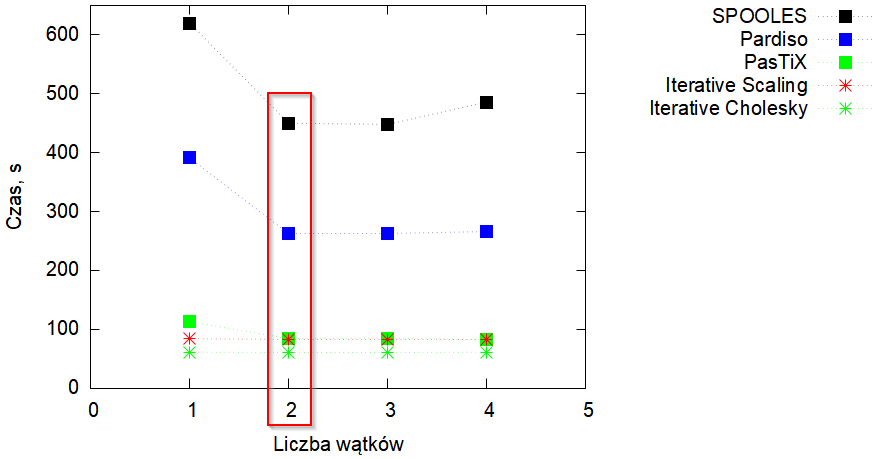 |
| Rys. 4. Zależność czasu rozwiązania zagadnienia od liczby wykorzystywanych wątków. Procesor i5-5300U |
Rys. 4 pokazuje zależność czasu rozwiązania zagadnienia od liczby wątków dla różnych solverów w przypadku modelu z maksymalną liczbą stopni swobody. Te wyniki uzyskane są dla procesora i5-5300U (5. generacja procesorów Intel Core (Broadwell), 2 rdzenie, 4 wątki). Najlepsze wyniki otrzymane są dla solveru PasTiX (6 razy szybszy od SPOOLES i 3-krotnie od Pardiso) i obydwu solverów iteracyjnych. Warto odnotować to, że prawie we wszystkich przypadkach najszybsze wyniki uzyskano przy 2. wątkach.
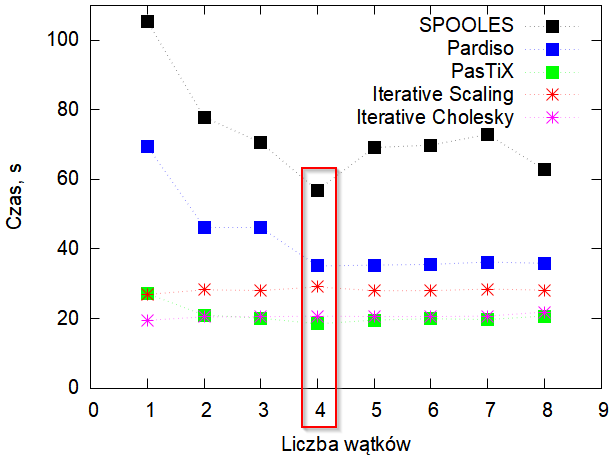 |
| Rys. 5. Zależność czasu rozwiązania zagadnienia od liczby wykorzystywanych wątków. Procesor i5-10210U. |
Podobne wyniki (Rys. 5) uzyskano dla bardziej wydajnego procesora i5-10210U (10 generacja procesorów Intel Core (Comet Lake), 4 rdzenie, 8 wątków). Tu ponownie używanie więcej niż połowy wątków nie pozwala uzyskać lepszy wynik, a czasem nawet go pogarsza.
4.2.1
Wnioski i zalecenia praktyczne
- Podstawowy wniosek – domyślne ustawienia, przy których do rozwiązania zagadnienia przypisana jest maksymalnie możliwa liczba wątków procesora są bezpieczne i pozwalają na szybkie obliczenia.
- Test pokazał, że przynajmniej dla procesorów rodziny Intel Core i5 do uzyskania maksymalnego przyspieszenia obliczeń można zmniejszyć liczę wątków. Wystarczy przypisać zmiennym środowiskowym CCX_NPROC_STIFFNESS, OMP_NUM_THREADS i CCX_NPROC_RESULTS wartość równą połowie maksymalnej liczby wątków, czyli wartość liczby rdzeni. Można to zrobić np. poprzez zamianę fragmentu odpowiedniego fragmentu pliku ccx_win*.cmd na
set /a CCX_NPROC_STIFFNESS=%NUMBER_OF_PROCESSORS%/2
set /a OMP_NUM_THREADS=%NUMBER_OF_PROCESSORS%/2
set /a CCX_NPROC_RESULTS=%NUMBER_OF_PROCESSORS%/2
Tu zmiany zaznaczone są na czerwono.
- Bardzo dobre wyniki uzyskane za pomocą iteracyjnych solverów są raczej wydatkiem niż regułą. Niestety tak dobrze jest tylko w przypadku liniowych zagadnień 3D z bardzo małymi wynikowymi przemieszczeniami i brakiem stref koncentracji naprężeń. We wszystkich pozostałych przypadkach czas obliczeń dla włączonych do CCX solverów iteracyjnych jest najdłuższy. Z tego powodu warto używać tylko solvery PasTiX lub Pardiso.
4.2.2
Przetestuj swój procesor
Wyniki testu pokazane wyżej dotyczą tylko dwóch procesorów Core i5. Dla procesorów innego typu (a szczególnie procesorów AMD) wynik może być inny. Warto dobrać optymalne parametry solverów dla posiadanego sprzętu. Szybki test można przeprowadzić w sposób następujący:
- Ściągnij i rozpakuj w dowolnym katalogu tymczasowymten plik

- W 5. wierszu każdego pliku *.CMD wpisz aktualną ścieżkę do katalogu zawierającego pliki CCX
- Uruchom po kolei CMD-pliki przynajmniej dla najbardziej przydatnych dla praktyki solverów PasTiX i Pardiso. W ten sposób zagadnienie testowe dla modelu z 207 500 stopniami swobody zostanie rozwiązane najpierw używając 1 wątku, później 2 itd. aż do maksymalnej liczby wątków dla danego procesora. Czas wymagany do rozwiązania każdego zadania zostanie zapisany do pliku *.LOGFILE. Przykładowy wynik pokazany jest niżej
Number of threads 1
Total CalculiX Time: 36.828916
Number of threads 2
Total CalculiX Time: 26.626712
Number of threads 3
Total CalculiX Time: 27.452315
Number of threads 4
Total CalculiX Time: 25.727938

|
Uwagi praktyczne.
- W czasie wykonywania testów lepiej nie uruchamiać inne programy. W przeciwnym razie wyniki będą wypatrzone.
- W większości laptopów wynik będzie zależał od tego, czy laptop jest podłączony do zasilania, czy pracuje na baterii. W drugim przypadku zwykle procesor pracuje wolniej.
- Do uzyskania najwyższej wydajności procesora można użyć specjalnych programów typu darmowego Quick CPU

|
4.3
Tempo wzrostu czasu obliczeń wraz ze zwiększeniem liczby równań równowagi
Czas wykonywania procedur obliczeniowych używanych w czasie rozwiązywania zagadnienia MES w różnym stopniu zależy od liczby stopni swobody modelu. Dla procedur obliczania macierzy sztywności poszczególnych elementów oraz wyznaczania odkształceń i naprężeń jest to zależność liniowa. W przypadku programów używanych do rozwiązywania układu równań równowagi analogiczna zależność jest kwadratową w przypadku solwerów dokładnych (direct) lub liniową w przypadku solwerów iteracyjnych. W wyniku tego ogólny czas obliczeń T dla solwerów iteracyjnych będzie liniowo zależał od liczby stopni swobody N (czyli T ~ N), a w przypadku solwerów dokładnych zależność ta będzie miała postać T ~ Nα, gdzie 1 < α < 2. Wartość wykładnika α będzie tym wyższa, im dłuższy czas zajmuje dla danego solwera dokładnego rozwiązanie układu równań.
 |
| Rys. 6. Zależność czasu rozwiązania zagadnienia od liczby stopni swobody modelu. Procesor i5-5300U. |
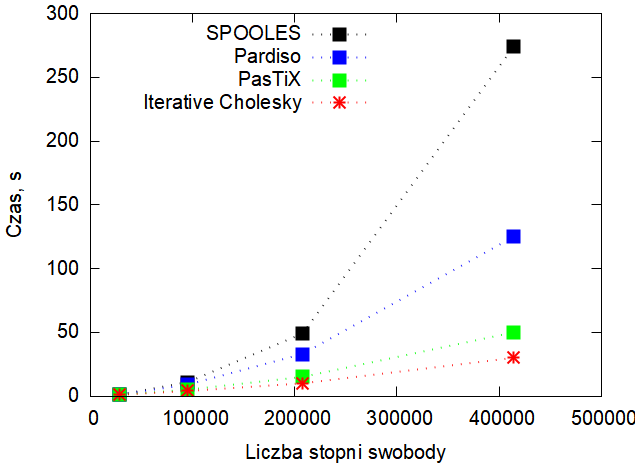 |
| Rys. 7. Zależność czasu rozwiązania zagadnienia od liczby stopni swobody modelu. Procesor i5-10210U. |
Na Rys. 6 i 7 pokazane są wyniki dla omawianego wyżej zagadnienia testowego. Widzimy, że czas obliczeń w przypadku metody iteracyjnej rośnie prawie liniowo. Dla metod dokładnych ta zależność jest już nieliniową.
|
Solver
|
Procesor i5-5300U
|
Procesor i5-10210U
|
| SPOOLES |
1,80 |
1,83 |
| Pardiso |
1,67 |
1,56 |
| PasTiX |
1,42 |
1,33 |
Tab. 1. Wartości wykładnika α dla różnych solverów i typów procesora.
Wartości wykładnika α podane w tabeli 1 pokazują, że najwolniej czas obliczeń rośnie dla najszybszego z solverów dokładnych PasTiX, a najszybciej – dla najwolniejszego SPOOLES. Obliczenia przeprowadzono dla optymalnej liczby wątków dla każdego z procesorów.
© I.Rokach, 2018-21, v.5.1.0, 24.08.2021, dla PrePoMax 1.1.0, Calculix 2.17
 . Licencja na niego została wykupiona przez Intel od pierwotnego producenta i zoptymalizowana pod procesory tejże firmy. Jest obecnie częścią darmowej biblioteki Intel openAPI MKL. To jest ten sam solver, który w SOLIDWORKS Simulation nazywa się Intel Direct Sparse. "Wyciska" maksimum z procesorów Intela, niestety ma niższą wydajność w przypadku procesorów AMD.
. Licencja na niego została wykupiona przez Intel od pierwotnego producenta i zoptymalizowana pod procesory tejże firmy. Jest obecnie częścią darmowej biblioteki Intel openAPI MKL. To jest ten sam solver, który w SOLIDWORKS Simulation nazywa się Intel Direct Sparse. "Wyciska" maksimum z procesorów Intela, niestety ma niższą wydajność w przypadku procesorów AMD.






